一、视觉定位系统基础矩阵的原理

　　介绍基础矩阵我们先说一下对积几和

　　对极几何一定是对二幅图像而言，对极几何实际上是“两幅图像之间的对极几何”，它是图像平面与以基线为轴的平面束的交的几何(这里的基线是指连接摄像机中心的直线)，以下图为例：对极几何描述的是左右两幅图像(点x和x’对应的图像)与以CC’为轴的平面束的交的几何!

　　直线CC’为基线，以该基线为轴存在一个平面束，该平面束与两幅图像平面相交，下图给出了该平面束的直观形象，可以看到，该平面束中不同平面与两幅图像相交于不同直线；

　　上图中的灰色平面π，只是过基线的平面束中的一个平面(当然，该平面才是平面束中最重要的、也是我们要研究的平面);

　　epipolarpoints极点

　　每一个相机的透镜中心是不同的，会投射到另一个相机像面的不同点上。这两个像点用eL和eR表示，被称为epipolarpoints极点。两个极点eL、eR分别与透镜中心OL、OR在空间中位于一条直线上。

　　epipolarplane极面

　　将X、OL和OR三点形成的面称为epipolarplane极面。

　　epipolarline极线

　　直线OL-X被左相机看做一个点，因为它和透镜中心位于一条线上。然而，从右相机看直线OL-X，则是像面上的一条线直线eR-XR，被称为epipolarline极线。从另一个角度看，极面X-OL-OR与相机像面相交形成极线。

　　极线是3D空间中点X的位置函数，随X变化，两幅图像会生成一组极线。直线OL-X通过透镜中心OL，右像面中对应的极线必然通过极点eR。一幅图像中的所有极线包含了该图像的所有极点。实际上，任意一条包含极点的线都是由空间中某一点X推导出的一条极线。

　　如果两个相机位置已知，则：

　　1.如果投影点XL已知，则极线eR-XR已知，点X必定投影到右像面极线上的XR处。这就意味着，在一个图像中观察到的每个点，在已知的极线上观察到该点的其他图像。这就是Epipolarconstraint极线约束：X在右像面上的投影XR必然被约束在eR-XR极线上。对于OL-XL上的X，X1，X2，X3都受该约束。极线约束可以用于测试两点是否对应同一3D点。极线约束也可以用两相机间的基本矩阵来描述。

　　2.如果XL和XR已知，他们的投影线已知。如果两幅图像上的点对应同一点X，则投影线必然交于X。这就意味着X可以用两个像点的坐标计算得到。

　　二、视觉定位系统基础矩阵

　　如果已知基础矩阵F，以及一个3D点在一个像面上的像素坐标p，则可以求得在另一个像面上的像素坐标p‘。这个是基础矩阵的作用，可以表征两个相机的相对位置及相机内参数。

　　面具体介绍基础矩阵与像素坐标p和p’的关系。

　　以O1为原点，光轴方向为z轴，另外两个方向为x，y轴可以得到一个坐标系，在这个坐标系下，可以对P，p1(即图中所标p)，p2(即图中所标p‘)得到三维坐标，同理，对O2也可以得到一个三维坐标，这两个坐标之间的转换矩阵为[RT]，即通过旋转R和平移T可以将O1坐标系下的点P1(x1，y1，z1)，转换成O2坐标系下的P2(x2，y2，z2)。

　　则可知，P2=R(P1-T)(1)

　　采用简单的立体几何知识，可以知道

　　其中，p，p‘分别为P点的像点在两个坐标系下分别得到的坐标(非二维像素坐标)。Rp’为极面上一矢量，T为极面上一矢量，则两矢量一叉乘为极面的法向量，这个法向量与极面上一矢量p一定是垂直的，所以上式一定成立。(这里采用转置是因为p会表示为列向量的形式，此处需要为行向量)

　　采用一个常用的叉乘转矩阵的方法，

　　将我们的叉乘采用上面的转换，会变成

　　红框中所标即为本征矩阵E，他描述了三维像点p和p‘之间的关系

　　有了本征矩阵，我们的基础矩阵也就容易推导了，

　　注意到将p和p‘换成P1和P2式(4)也是成立的，且有

　　q1=K1P1(6)

　　q2=K2P2(7)

　　上式中，K1K2为相机的校准矩阵，描述相机的内参数q1q2为相机的像素坐标代入式(4)中，得

　　上式中p->q1，p‘->q2

　　这样我们就得到了两个相机上的像素坐标和基础矩阵F之间的关系了

　　二、不同图像对的基础矩阵

　　代码

　　# coding: utf-8

　　# In[1]:

　　from PIL import Image

　　from numpy import *

　　from pylab import *

　　import numpy as np

　　# In[2]:

　　from PCV.geometry import homography, camera, sfm

　　from PCV.localdescriptors import sift

　　# In[5]:

　　# Read features

　　im1 = array(Image.open('im1.jpg'))

　　sift.process_image('im1.jpg', 'im1.sift')

　　im2 = array(Image.open('im2.jpg'))

　　sift.process_image('im2.jpg.', 'im2.sift')

　　# In[6]:

　　l1, d1 = sift.read_features_from_file('im1.sift')

　　l2, d2 = sift.read_features_from_file('im2.sift')

　　# In[7]:

　　matches = sift.match_twosided(d1, d2)

　　# In[8]:

　　ndx = matches.nonzero()[0]

　　x1 = homography.make_homog(l1[ndx, :2].T)

　　ndx2 = [int(matches[i]) for i in ndx]

　　x2 = homography.make_homog(l2[ndx2, :2].T)

　　d1n = d1[ndx]

　　d2n = d2[ndx2]

　　x1n = x1.copy()

　　x2n = x2.copy()

　　# In[9]:

　　figure(figsize=(16,16))

　　sift.plot_matches(im1, im2, l1, l2, matches, True)

　　show()

　　# In[10]:

　　#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):

　　def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):

　　""" Robust estimation of a fundamental matrix F from point

　　correspondences using RANSAC (ransac.py from

　　http://www.scipy.org/Cookbook/RANSAC).

　　input: x1, x2 (3*n arrays) points in hom. coordinates. """

　　from PCV.tools import ransac

　　data = np.vstack((x1, x2))

　　d = 10 # 20 is the original

　　# compute F and return with inlier index

　　F, ransac_data = ransac.ransac(data.T, model,

　　8, maxiter, match_threshold, d, return_all=True)

　　return F, ransac_data['inliers']

　　# In[11]:

　　# find F through RANSAC

　　model = sfm.RansacModel()

　　F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-3)

　　print(F)

　　# In[12]:

　　P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])

　　P2 = sfm.compute_P_from_fundamental(F)

　　# In[13]:

　　print(P2)

　　print(F)

　　# In[14]:

　　# P2, F (1e-4, d=20)

　　# [[ -1.48067422e+00 1.14802177e+01 5.62878044e+02 4.74418238e+03]

　　# [ 1.24802182e+01 -9.67640761e+01 -4.74418113e+03 5.62856097e+02]

　　# [ 2.16588305e-02 3.69220292e-03 -1.04831621e+02 1.00000000e+00]]

　　# [[ -1.14890281e-07 4.55171451e-06 -2.63063628e-03]

　　# [ -1.26569570e-06 6.28095242e-07 2.03963649e-02]

　　# [ 1.25746499e-03 -2.19476910e-02 1.00000000e+00]]

　　# In[15]:

　　# triangulate inliers and remove points not in front of both cameras

　　X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)

　　# In[16]:

　　# plot the projection of X

　　cam1 = camera.Camera(P1)

　　cam2 = camera.Camera(P2)

　　x1p = cam1.project(X)

　　x2p = cam2.project(X)

　　# In[17]:

　　figure(figsize=(16, 16))

　　imj = sift.appendimages(im1, im2)

　　imj = vstack((imj, imj))

　　imshow(imj)

　　cols1 = im1.shape[1]

　　rows1 = im1.shape[0]

　　for i in range(len(x1p[0])):

　　if (0<= x1p[0][i]

　　plot([x1p[0][i], x2p[0][i]+cols1],[x1p[1][i], x2p[1][i]],'c')

　　axis('off')

　　show()

　　# In[18]:

　　d1p = d1n[inliers]

　　d2p = d2n[inliers]

　　# In[19]:

　　# Read features

　　im3 = array(Image.open('im3.jpg'))

　　sift.process_image('im3.jpg', 'im3.sift')

　　l3, d3 = sift.read_features_from_file('im3.sift')

　　# In[20]:

　　matches13 = sift.match_twosided(d1p, d3)

　　# In[21]:

　　ndx_13 = matches13.nonzero()[0]

　　x1_13 = homography.make_homog(x1p[:, ndx_13])

　　ndx2_13 = [int(matches13[i]) for i in ndx_13]

　　x3_13 = homography.make_homog(l3[ndx2_13, :2].T)

　　# In[22]:

　　figure(figsize=(16, 16))

　　imj = sift.appendimages(im1, im3)

　　imj = vstack((imj, imj))

　　imshow(imj)

　　cols1 = im1.shape[1]

　　rows1 = im1.shape[0]

　　for i in range(len(x1_13[0])):

　　if (0<= x1_13[0][i]

　　plot([x1_13[0][i], x3_13[0][i]+cols1],[x1_13[1][i], x3_13[1][i]],'c')

　　axis('off')

　　show()

　　# In[23]:

　　P3 = sfm.compute_P(x3_13, X[:, ndx_13])

　　# In[24]:

　　print(P3)

　　# In[25]:

　　print(P1)

　　print(P2)

　　print(P3)

　　# In[26]:

　　# Can't tell the camera position because there's no calibration matrix (K)

　　得到视觉对位系统基础矩阵如下

　　室外

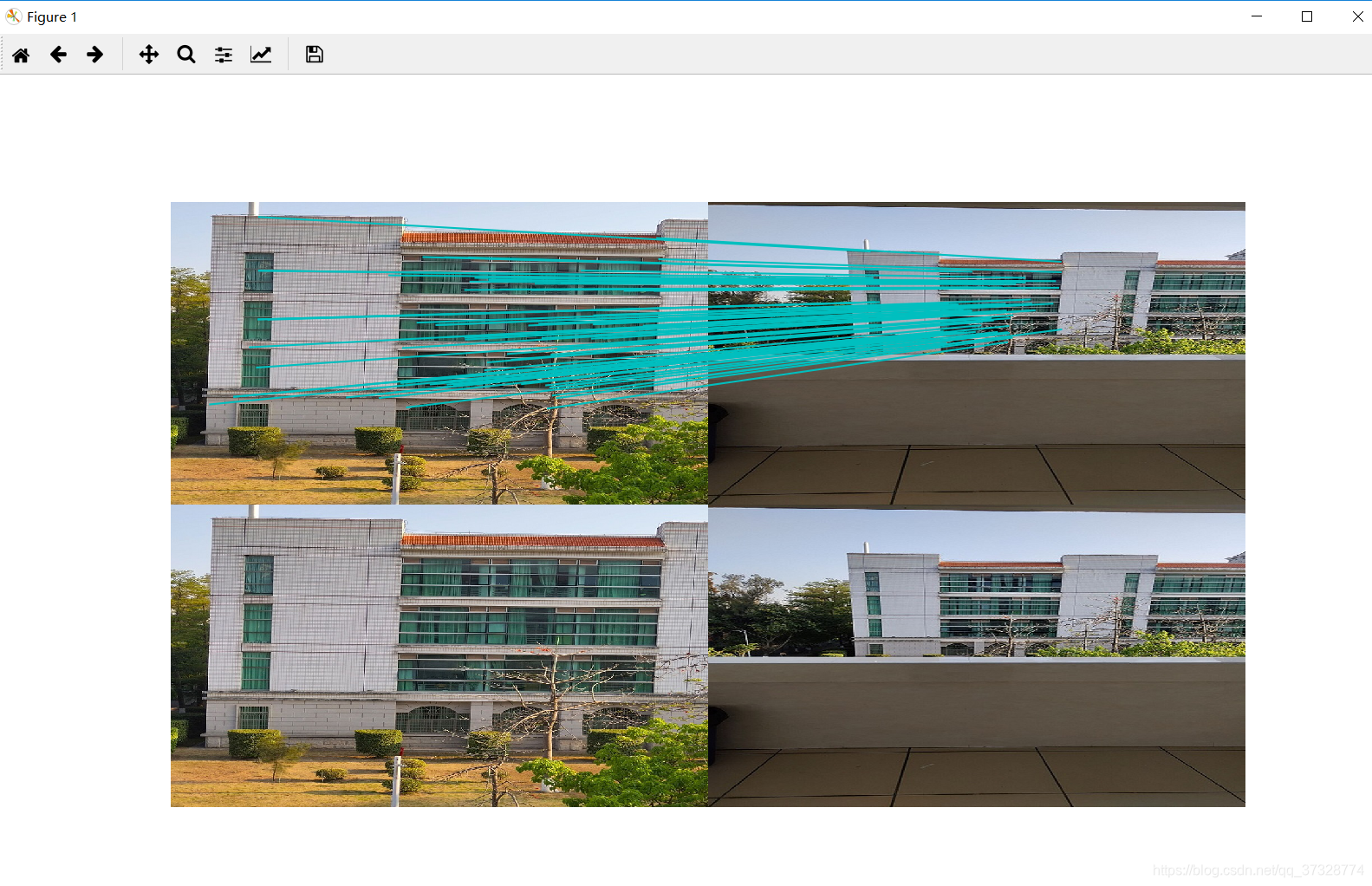
　　得到基础矩阵如下